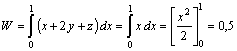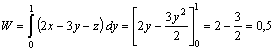ENSEÑANZA
DE LA FÍSICA Y LA QUÍMICA
sección:
DIDÁCTICA DE LA FÍSICA Y LA QUÍMICA
INTRODUCCIÓN
A LA TEORÍA DE CAMPOS III
10. CIRCULACIÓN DEL VECTOR CAMPO: CAMPOS
CONSERVATIVOS.
CONCEPTOS.
Cuando hacemos recorrer el vector campo
(intensidad de un campo), a lo largo de una línea (un camino, con elemento
infinitesimal
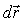 ), se define la CIRCULACIÓN DE DICHO VECTOR como:
), se define la CIRCULACIÓN DE DICHO VECTOR como:
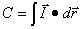 (19)
(19)
o sea la integral a lo largo del recorrido
efectuado, del producto escalar de la intensidad del campo por el vector desplazamiento.
Es una magnitud escalar por proceder de un producto escalar.
Entre dos puntos a y b sería:
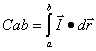 (20)
(20)
Si el recorrido se efectúa sobre una línea
cerrada la expresión sería:
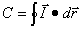 (muchas veces se reserva
el nombre de CIRCULACIÓN específicamente para este recorrido, aplicando el
de PROCESIÓN, cuando es abierto).
(muchas veces se reserva
el nombre de CIRCULACIÓN específicamente para este recorrido, aplicando el
de PROCESIÓN, cuando es abierto).
Dado que por definición
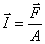 , al sustituir en la expresión
, al sustituir en la expresión
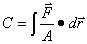 . Al definirse el trabajo
W como
. Al definirse el trabajo
W como
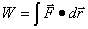 , tendremos que la circulación del vector campo
no es más que:
, tendremos que la circulación del vector campo
no es más que:
EL
TRABAJO POR UNIDAD DE MAGNITUD ACTIVA
Vamos a aplicar los conceptos anteriores
y calcular la circulación de
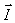 desde A hasta B, y luego desde B hasta A en el dibujo dado (fig.42)
desde A hasta B, y luego desde B hasta A en el dibujo dado (fig.42)
Si la intensidad es tal, que se mantiene
constante, es evidente que al ir de A hasta B, el desplazamiento
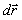 , tendrá sentido contrario al efectuado al regresar a A, y por lo tanto siendo
un producto escalar, el ángulo será suplementario, y el coseno, de signo contrario
Como su módulo es el mismo, ocurrirá que al sumarlo se anularán, siendo
la circulación total nula. Los campos vectoriales en los que la circulación
del vector campo a lo largo de un recorrido cerrado es nula, se denominan
CAMPOS CONSERVATIVOS.
, tendrá sentido contrario al efectuado al regresar a A, y por lo tanto siendo
un producto escalar, el ángulo será suplementario, y el coseno, de signo contrario
Como su módulo es el mismo, ocurrirá que al sumarlo se anularán, siendo
la circulación total nula. Los campos vectoriales en los que la circulación
del vector campo a lo largo de un recorrido cerrado es nula, se denominan
CAMPOS CONSERVATIVOS.
Si consideramos un campo de gradientes,
como podría ser el de alturas esto es aquél en que
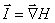 y lo hacemos circular a lo largo de una línea
cerrada, tendríamos que
y lo hacemos circular a lo largo de una línea
cerrada, tendríamos que
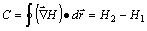 , como coincide la altura
final con la inicial, al ser el recorrido cerrado, C= 0, y el campo será CONSERVATIVO.
Por lo tanto todo campo cuya intensidad sea el gradiente de una función
(llamada función potencial), será siempre CONSERVATIVO.
, como coincide la altura
final con la inicial, al ser el recorrido cerrado, C= 0, y el campo será CONSERVATIVO.
Por lo tanto todo campo cuya intensidad sea el gradiente de una función
(llamada función potencial), será siempre CONSERVATIVO.
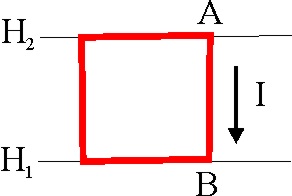
Fig.42
¿Cómo
sabremos cuándo un campo es conservativo?
a) Si su
intensidad deriva de una función potencial a través de su gradiente.
b) Si la
circulación de su intensidad no depende del camino
c) Si la
circulación de su intensidad en un recorrido cerrado es 0.
10.1.
APLICACIÓN: DETERMINACIÓN DE UN CAMPO CONSERVATIVO
La circulación se calcularía exactamente
igual que el trabajo, si la magnitud activa que crea el campo es la unidad
o sea a través del proceso de integración de un producto escalar, considerando
que:
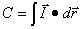 y que
y que
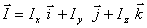 , mientras
que
, mientras
que
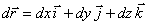
Si se realiza el producto escalar, y se
separa en integrales tendremos que:
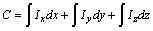 (21)
(21)
Al resolver cada integración, todo lo que
no sea la variable será considerado constante.
APLICACIÓN
Ej14. Dado el campo vectorial
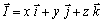 , determina su circulación en el paralelepípedo de la figura 43, desde O hasta
A, a través de los siguientes caminos
, determina su circulación en el paralelepípedo de la figura 43, desde O hasta
A, a través de los siguientes caminos
1) OCBA 2) OGFA. 3) OEDA
Verificando si se trata o no de un campo conservativo.
FÓRMULA A APLICAR:
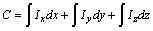
PASOS A SEGUIR:
a) Se
efectúa el producto escalar, con lo que la expresión de la circulación es
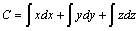
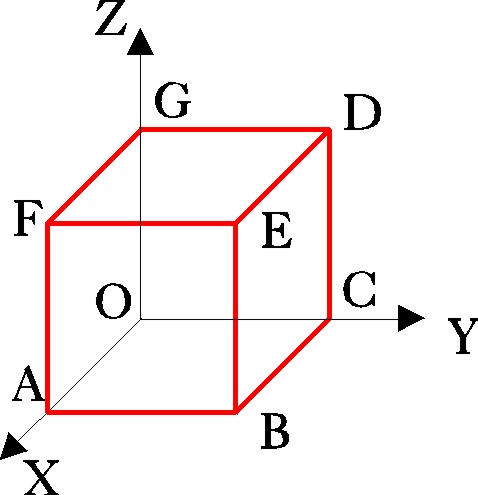
Fig.43
b) Se lleva la expresión al camino tratado, y puesto que las aristas
sobre los ejes X (a), Y (b) y Z(c), al integrar para estos valores produciría
una circulación, para cualquiera de los recorridos dados C = a2/2 + b2/2 + c2/2.
c) Conclusión: SE TRATA DE UN CAMPO CONSERVATIVO (la circulación no
depende del camino)
Ej15 Un cierto campo de fuerzas viene dado por la expresión
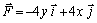 . Determina el trabajo desarrollado por la fuerza al desplazarse desde el
punto (0,0) al (2,2), por el camino OAB y por el OCB, justificando su carácter
conservativo o no conservativo (fig.44)
. Determina el trabajo desarrollado por la fuerza al desplazarse desde el
punto (0,0) al (2,2), por el camino OAB y por el OCB, justificando su carácter
conservativo o no conservativo (fig.44)
FÓRMULA A APLICAR:
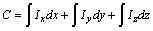 .
.
PASOS A SEGUIR:
a) Se efectúa el producto escalar, con lo que la expresión de la circulación
es
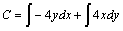 . Se lleva la expresión a cada
camino.
. Se lleva la expresión a cada
camino.
b) En OBA. Primero, en OB, x
varía entre 0 y 2 y y = 0, por lo que COB = 0.
En BA, x es constante = 2, e y varía entre 0 y 2, por
lo que
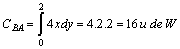
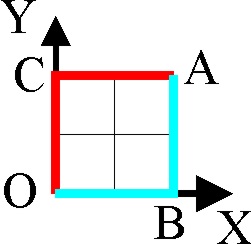
Fig.44
c) En OCA. Primero, en OC, x= 0 , e y varía entre 0 y 2, por lo que
COC = 0.
En CA, y es constante = 2 , y x varía entre 0 y 2, por
lo que
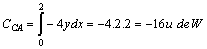
d) Conclusión: EL CAMPO NO ES
CONSERVATIVO porque la circulación entre O y A no es la misma por caminos
distintos, o sea depende del camino
10.2.
MÉTODOS GRÁFICOS PARA CONOCER SI UN
CAMPO ES O NO CONSER-VATIVO.
Se puede calcular a través de métodos gráficos
si un campo es o no conservativo, si se conoce el dibujo de la intensidad
o las líneas de fuerza. Para ello se elige un recorrido cerrado, y se efectúa
a lo largo de ese recorrido, la circulación del vector campo, si es nula,
se tratará de un campo conservativo
Ej16 Dadas las líneas de fuerza y los vectores campos, de la figura
45, justifica si se trata o no de un campo conservativo.
PASOS A SEGUIR:
a) Siguiendo los ejemplos anteriores, se realizan las circulaciones
parciales, eliminando las que se anulan, por ser perpendiculares intensidades
y desplazamientos.
b) Si los caminos son iguales, observaríamos que la circulación total
nunca sería nula, por lo que el campo NO SERÍA CONSERVATIVO.
Ej17. ¿Será conservativo
un campo radial divergente creado por una magnitud activa puntual, como el dado por
la figura 46?
PASOS A SEGUIR:
a) Se busca un itinerario para hacer circular el vector campo, en este
caso al ser radial es conveniente elegir circunferencias, para eliminar la
circulación en dichos tramos, ya que al ser radial ,
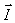 y
y
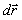 son perpendiculares en esos tramos (BC y DA)
y su producto escalar es nulo.
son perpendiculares en esos tramos (BC y DA)
y su producto escalar es nulo.
b) La circulación sólo no se anula en los tramos AB y CD. En AB, el vector campo y el desplazamiento
forman un ángulo de 0º, mientras que en CD, el ángulo es de 180º, y su coseno
-1. Por este motivo, la circulación total es nula, y el campo CONSERVATIVO.
Ej18 Comprobar que el campo gravitatorio es conservativo, a través
de la constancia de la circulación entre O (0,0) y B(2,2), por los dos caminos
dados (fig.47).
PASOS A SEGUIR:
a) Dado que la intensidad del campo gravitatorio es -g j .
Por el camino inferior OAB:
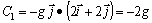
b) Por el camino superior OB:
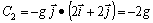 , tendremos el mismo resultado anterior.
, tendremos el mismo resultado anterior.
c) Conclusión el campo es CONSERVATIVO.
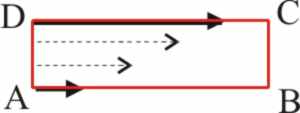
Fig.45
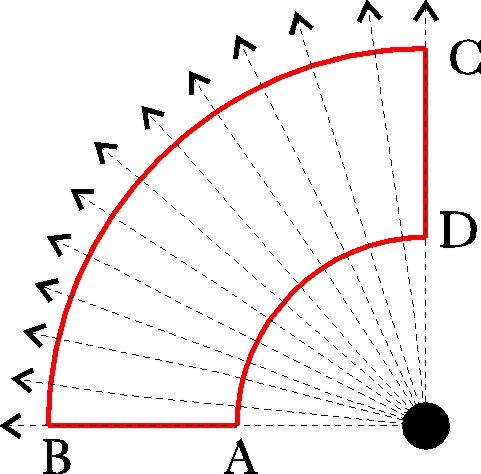
Fig.46
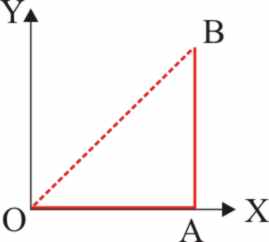
Fig.47
Cuando un campo es conservativo ¿Qué se
conserva? Sencillamente la energía mecánica, que sólo se va transformando,
de tal forma que no dependa del camino empleado en dicha transformación, las
fuerzas del campo son FUERZAS CONSERVATIVAS. Es evidente que en la realidad
existen fuerzas que disipan la energía: FUERZAS DISIPATIVAS, en este caso
si se consideraran no se comportaría como campo conservativo. En la realidad
el campo gravitatorio, debido al rozamiento con fluidos, no sería conservativo;
sólo en el vacío. Conviene tener en cuenta que la energía térmica, es una
forma de energía mecánica, pues se debe al movimiento caótico de las moléculas,
y por lo tanto la conversión en energía interna de un sistema, o energía cinética
interna, no produce efectos disipativos, actuando el campo de forma conservativa.
Es el caso de una catarata en un río. Las
moléculas de agua poseen una velocidad (energía cinética), y una energía potencial,
en la parte alta de la catarata. En la inferior, al producirse la caída del
agua, con el consabido calentamiento, no ha habido pérdida teórica de energía,
salvo la que se produzca por disipación a causa del rozamiento por aumento de velocidad, con el propio cauce.
De esta forma, se conservaría la energía como se aprecia en el dibujo (fig.48),
y el campo pese al desplazamiento que ha habido de las moléculas de agua ha
actuado de forma conservativa.
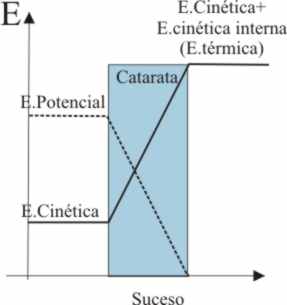
Fig.48
Ej19. ¿Las fuerzas centrales son conservativas?
CONSIDERACIONES
Un cuerpo sometido a fuerza centrales, y por lo tanto con una aceleración
centrípeta, puede describir un movimiento circular (simplificado), o elíptico,
como ocurre con el electrón en el átomo de hidrógeno, o la Tierra alrededor
del Sol (fig.49)
PASOS A SEGUIR
a) Se dibuja la trayectoria circular, y la aceleración normal. La fuerza
actuante es perpendicular por dicho motivo en cada instante a la trayectoria.
b) El desplazamiento infinitesimal a lo largo de dicha trayectoria,
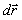 tangente a la trayectoria, en cada instante,
es perpendicular a dicha fuerza central.
tangente a la trayectoria, en cada instante,
es perpendicular a dicha fuerza central.
c) Como
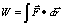 , y el ángulo formado por los vectores
es de 90º, su coseno es 0, con lo cual W=0. Por lo tanto las fuerzas centrales
no hacen trabajo, la circulación a lo largo de la circunferencia es nula
y las fuerzas serán conservativas.
, y el ángulo formado por los vectores
es de 90º, su coseno es 0, con lo cual W=0. Por lo tanto las fuerzas centrales
no hacen trabajo, la circulación a lo largo de la circunferencia es nula
y las fuerzas serán conservativas.
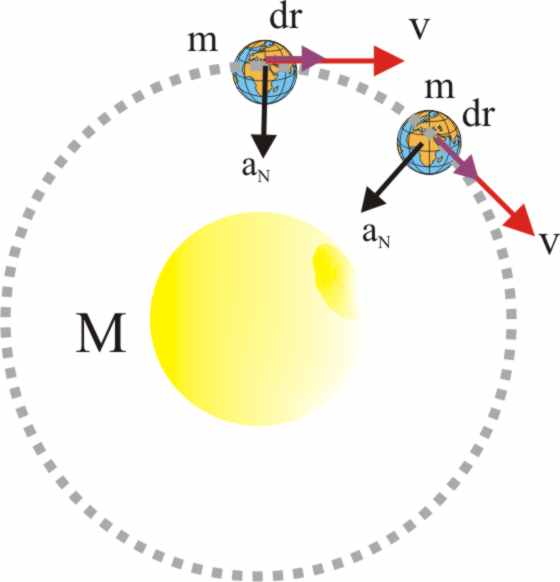
Fig.49
10.3.
OTROS PROCEDIMIENTOS PARA CONOCER SI UN CAMPO ES CONSERVATIVO: EL ROTACIONAL
DE UN CAMPO
La determinación del carácter conservativo
de un campo, implica el cálculo de la circulación o del trabajo, por dos caminos
diferentes o en una trayectoria cerrada, lo cual implica si la intensidad
es variable, un desarrollo integral. Ahora bien, existe un operador matemático
denominado ROTACIONAL, que lo simplifica: El ROTACIONAL DE UN CAMPO se define como:
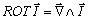 (22)
(22)
esto es el producto vectorial del nabla
por la intensidad del campo.
Por otra parte, el rotacional hace referencia
a la circulación del vector campo a lo largo de una trayectoria cerrada que
encierra determinada superficie, por lo que
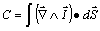 (23)
(23)
Esta es la expresión más simple del teorema
de Stokes, que permite calcular la circulación de otra forma. Lo interesante
es que si la circulación es 0 (campo conservativo), el ROTACIONAL TAMBIÉN LO SERÁ, por lo que se puede
definir un campo conservativo como aquél cuyo ROTACIONAL ES NULO;
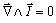 (24), también llamada irrotacional.
(24), también llamada irrotacional.
Al hacer
el producto vectorial del nabla
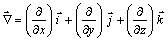 por la intensidad del campo
por la intensidad del campo
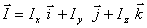 e igualar
a 0 cada componente, nos queda como
condición de CAMPO CONSERVATIVO que:
e igualar
a 0 cada componente, nos queda como
condición de CAMPO CONSERVATIVO que:
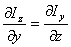
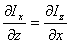
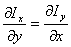 (25)
(25)
Dicho en otras palabras las "derivadas
cruzadas deben ser iguales". Para que se cumpla esta condición de conservativo,
deberán darse las tres igualdades, en el caso de existir 3 componentes. Por
todo lo dicho los campos CONSERVATIVOS, también reciben el nombre de IRROTACIONALES,
mientras que los NO CONSERVATIVOS, lo son ROTACIONALES, como el magnético.
En estos campos, la intensidad depende del llamado potencial vector A, de forma que
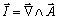
APLICACIÓN
Ej20. Dado el campo
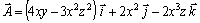 , demuestra que es conservativo
, demuestra que es conservativo
CONSIDERACIÓN PREVIA: Todo lo que no sea la variable respecto a la
que se deriva SE CONSIDERARÁ CONSTANTE
PASOS A SEGUIR:
a) Se aislan las componentes del campo: Ix = (4xy - 3x2z2)
; Iy = 2x2 ; Iz = - 2x3z
b) Derivada de la componente x del campo respecto a y, será igual a
la derivada de la componente y del campo respecto a x, o sea 4x = 4x
c) Derivada de la componente x del campo respecto a z, será igual a
la derivada de la componente z del campo respecto a x, o sea -6x2z = -6x2z
d) Derivada de la componente y del campo respecto a z, será igual a
la derivada de la componente z del campo respecto a y, o sea 0= 0
e) Por lo tanto como se producen las tres igualdades, el campo SERÁ
CONSERVATIVO.
En el caso de no hacerlo así, se tendría que hacer circular el vector
campo, por dos caminos diferentes y determinar que la circulación no depende
del camino, esto es como en el ejemplo 12.
Ej21. Dado el campo
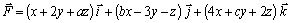 , determinar los valores de a,b y c, para que el campo sea conservativo.
, determinar los valores de a,b y c, para que el campo sea conservativo.
PASOS A SEGUIR:
a) Se aislan las componentes del campo: Fx = x + 2y + az ; Fy = bx
- 3y - z
Fz = 4x + cy + 2z
b) Se derivan parcialmente de forma "cruzada", tal como en
el caso anterior, igualando las expresiones. Así : a = 4 b = 2 c = -1
c) Se podría sustituir y comprobar si se trata o no de un campo conservativo:
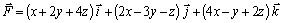
Calculando el trabajo por dos caminos
diferentes, siguiendo el esquema del ejemplo 12. Por ejemplo, calculando el
trabajo para ir de O hasta E, supuesto el lado del cubo igual a 1 (fig.50)
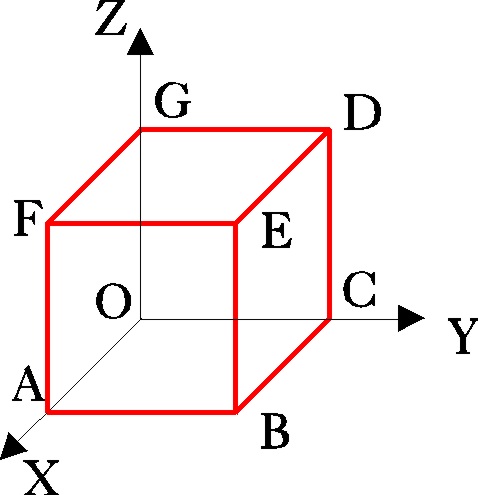
Fig.50
Como
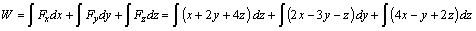 Camino1 : OCDE
Camino1 : OCDE
En OC , x=0 , z= 0 e y varía entre 0 y 1; por lo que
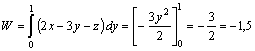
En CD
, y=1 = cte ; (dy=0), x=0 y z varía
entre 0 y 1, por lo que
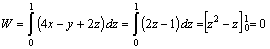
En DE, y=1=
cte (dy=0) , z=1= cte (dz=0) , y x varía entre 0 y 1, por lo que:
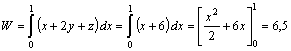 . El trabajo total será -1,5 + 6,5
+ 0 = 5 u. de trabajo.
. El trabajo total será -1,5 + 6,5
+ 0 = 5 u. de trabajo.
Camino 2 : OABE
En OA, y=0 , z=0 , y x varía entre 0 y 1 por lo que
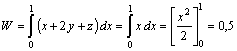
En AB
, x=1= cte ( dx=0) , z= 0 e y varía entre 0 y 1;
por lo que
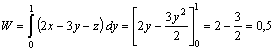
En BE , y=1 = cte ; (dy=0), x=1 (dx=0) y z varía entre 0 y 1, por lo que
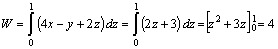
El trabajo total será 0,5 + 0,5 + 3 = 5 u. de
trabajo. EL CAMPO ES CONSERVATIVO.
Hemos visto que todo campo cuya intensidad
sea el gradiente de una función escalar, denominada función potencial o simplemente
potencial V, es un campo conservativo. Por lo tanto si
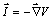 , vamos a demostrar que
este campo cumple que
, vamos a demostrar que
este campo cumple que
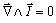
a) Desde el punto de vista del producto vectorial
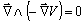 . Porque el nabla y el
-nabla de V, forman un ángulo de 180º, cuyo seno vale 0.
. Porque el nabla y el
-nabla de V, forman un ángulo de 180º, cuyo seno vale 0.
b) Si se realiza el producto vectorial a través
del determinante respectivo, se observará que tiene dos filas iguales, por
lo que también debe valer 0.
En consecuencia : TODO CAMPO CONSERVATIVO
TIENE UNA INTENSIDAD QUE ES EL GRADIENTE DE UNA FUNCIÓN POTENCIAL CON EL SIGNO CONTRARIO (convenio de signos).
10.4.
EL OPERADOR DIVERGENCIA Y LOS CAMPOS CONSERVATIVOS
Si en
un campo conservativo
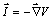 ¿Cuánto vale su divergencia
y qué significado tiene?
¿Cuánto vale su divergencia
y qué significado tiene?
La operación
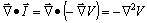 . Esta operación, prescindiendo del signo, se denomina actualmente laplaciana y se puede expresar
como :
. Esta operación, prescindiendo del signo, se denomina actualmente laplaciana y se puede expresar
como :
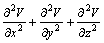
Se ha visto que
a) Para campos divergentes (ELÉCTRICO)
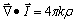 o
o
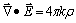
b) Para campos convergentes (GRAVITATORIO)
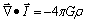 o
o
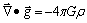
Al aplicar el concepto de laplaciana, y
sustituyendo k:
Para campos divergentes, como el creado
por la carga positiva,
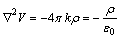
Teniendo en cuenta que
Si lo creara la carga negativa, cambiaría
de signo
Para campos divergentes, como el creado
por la masa,
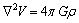
Estas ecuaciones se denominan de Poisson.
En regiones donde no existe magnitud activa,
y por lo tanto la densidad volúmica
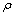 , es nula, las ecuaciones anteriores de Poisson, se transforman en
, es nula, las ecuaciones anteriores de Poisson, se transforman en
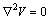 , que se conoce como ecuación de Laplace.
, que se conoce como ecuación de Laplace.
Actualmente el
operador laplaciano,
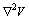 o divergencia del gradiente
o divergencia del gradiente
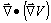 , se puede simbolizar por
, se puede simbolizar por
 , aunque pueda confundirse con el de incremento.
, aunque pueda confundirse con el de incremento.
11.
POTENCIAL
DE UN CAMPO CONSERVATIVO
Hemos visto que
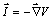 , lo que en campos radiales,
esto es, aquellos creados por magnitudes activas puntuales, se podría disponer
, lo que en campos radiales,
esto es, aquellos creados por magnitudes activas puntuales, se podría disponer
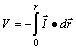 , lo cual nos dará la diferencia
de potencial entre dos puntos, uno de ellos el de referencia O.
, lo cual nos dará la diferencia
de potencial entre dos puntos, uno de ellos el de referencia O.
Como
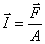 y
y
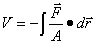 , pero como
, pero como
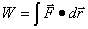 , la diferencia de potencial entre dos puntos a y b sería el TRABAJO PARA LLEVAR LA UNIDAD
DE MAGNITUD ACTIVA DE UN PUNTO DE REFERENCIA O a OTRO, PERO CON EL SIGNO CONTRARIO.
(A = 1).
, la diferencia de potencial entre dos puntos a y b sería el TRABAJO PARA LLEVAR LA UNIDAD
DE MAGNITUD ACTIVA DE UN PUNTO DE REFERENCIA O a OTRO, PERO CON EL SIGNO CONTRARIO.
(A = 1).
Para determinar el potencial en un punto,
conviene tomar una referencia 0, esto es un punto en el que el potencial sea
0, o donde las interacciones sean nulas; este punto es el infinito. Por este
motivo y teniendo en cuenta que tiene un signo menos delante, supone una inversión
en los límites de la integración, se podría definir el potencial en un punto
como:
EL TRABAJO PARA LLEVAR LA UNIDAD DE MAGNITUD
ACTIVA DESDE EL INFINITO AL PUNTO y coincide con la energía potencial en ese punto
LA ENERGÍA POTENCIAL ES IGUAL AL POTENCIAL
por la CANTIDAD DE MAGNITUD ACTIVA (Ep = A.V).
Por lo tanto el trabajo para llevar una
determinada cantidad de magnitud activa desde A hasta B, correspondería a
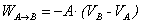 .
.
Cambiando los signos: W = AVA - AVB = Energía potencial inicial – Energía potencial
final. (26)
Por lo general esa cantidad de magnitud
activa que se sitúa en un campo, para comprobar sus efectos, y que es independiente
de la creadora del campo, es lo que se denomina MAGNITUD ACTIVA DE PRUEBA, y que en el campo eléctrico
sería la CARGA DE PRUEBA (siempre refiriéndose a carga positiva). Suele ser
pequeña, y en el límite hace referencia a la unidad de magnitud activa.
Las líneas y superficies en las que el potencial
del campo es constante, se denominan LÍNEAS DE POTENCIAL y SUPERFICIES EQUIPOTENCIALES,
respectivamente.
En los campos newtonianos (fuerza de interacción
inversamente proporcional al cuadrado de la distancia), es muy fácil determinar
la función potencial, debido a su simetría
radial (magnitudes activas puntuales o consideradas como puntuales). Así
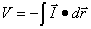 , como
, como
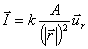 ,
,
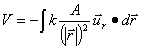 (28)
(28)
que producirá, una vez realizado el producto
escalar y la integral una expresión del potencial:
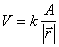 (29)
(29)
a) Si el campo es DIVERGENTE, como el ELÉCTRICO,
(A= q>0 ),
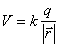 (30) en Voltio o J C-1
(30) en Voltio o J C-1
b) Si el campo es CONVERGENTE, como el GRAVITATORIO,
(A= m, k = -G) ,
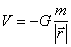 (31)
en N.m kg-1 o J kg-1
(31)
en N.m kg-1 o J kg-1
c)
Si el campo es CONVERGENTE, como el ELÉCTRICO (A = q<0 ),
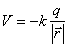
En todo caso para una determinada cantidad
de magnitud activa la expresión V.
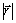 = cte, lo cual en gráficas (V, r) , corresponde a una HIPÉRBOLA EQUILÁTERA
(fig. 51 y 52)
= cte, lo cual en gráficas (V, r) , corresponde a una HIPÉRBOLA EQUILÁTERA
(fig. 51 y 52)
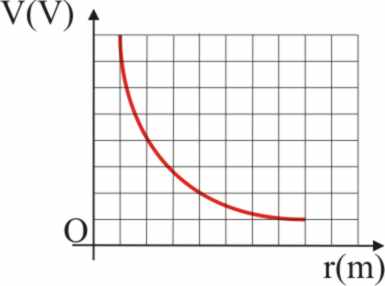
Fig.51
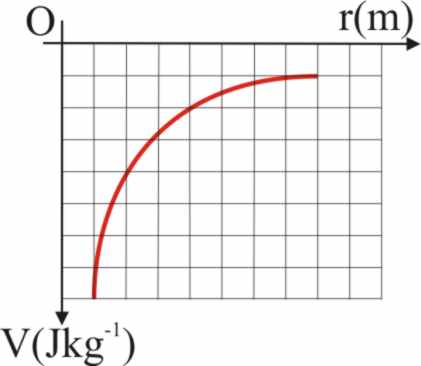
Fig.52
Como únicamente dependen del radio, las
líneas de igual potencial o líneas de potencial (líneas isotímicas) serán
CIRCUNFERENCIAS CONCÉNTRICAS.
¿Qué diferencias hay entre las variaciones
del potencial y las del campo respecto
a la distancia en el campo eléctrico para distribuciones de magnitudes activas
puntuales o esféricas?
Se
podrían determinar las pendientes respectivas a partir de las expresiones
V
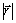 = kq y
Er2=kq
= kq y
Er2=kq
En
la gráfica (V, r) Vdr
+ rdV = 0 , de lo que dV/dr = - V/r (que
sería la pendiente)
En
la gráfica (E, r) r2dE
+ 2rdrE=0, de lo que dE/dr = - 2 E/r (que sería la pendiente).
como
E=-dV/dr, dE/dr =
2/r(dV/dr), que sería la relación entre ambas pendientes.
11.1.
DIFERENCIA DE POTENCIAL. CÁLCULO GRÁFICO
La diferencia de potencial entre dos puntos
A y B, para distribuciones de magnitudes activas puntuales o esféricas se
podría calcular fácilmente a partir de las propias gráficas:
APLICACIÓN
Ej.22. En las gráficas dadas calcula la diferencia de potencial entre
los puntos A y B, separados una distancia de 2m.
Para la gráfica 53 (potencial creado por un conductor con carga positiva
q, de radio R), la diferencia de potencial entre los puntos A y B, separados
2 metros será: VB-VA=20-40=-20V
Mientras que en la gráfica 54 (potencial creado por una masa M, o
una carga negativa q), la diferencia de potencial ente los puntos A y B, separados
2m, será: -20-(-40)=20V o 20Jkg-1.
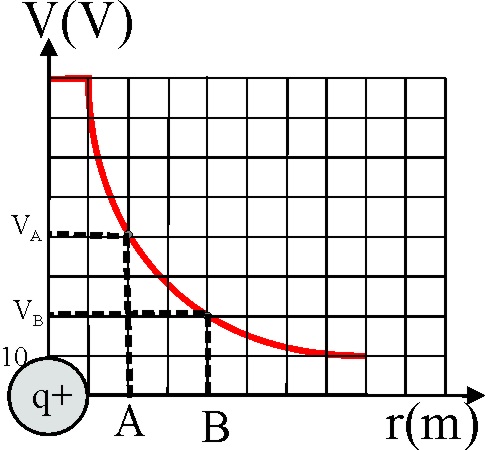
Fig.53
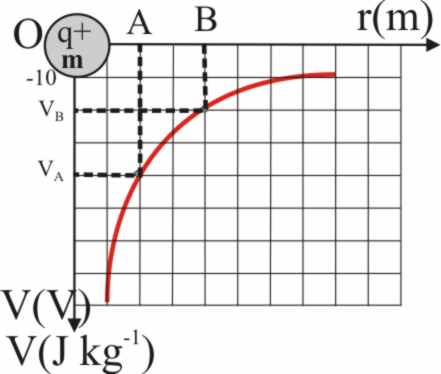
Fig.54
Ej. 23. Relación entre las gráficas (V, r ) y (E, r), para el campo
eléctrico creado por un conductor esférico de radio R=2m , con carga superficial
q. Comprobar su relación y determinar gráficamente el campo y el potencial a los 4m.
En la gráfica (V, r) debido al campo creado por un conductor esférico
de radio R=2m con carga superficial q, la pendiente para r>R dV/dr, nos
daría la intensidad del campo con el signo cambiado, al ser un campo conservativo,
E=- dV/dr.
Por lo tanto trazando la tangente en un punto (4m), (fig.55) podríamos
conocer la intensidad del campo en dicho punto:
-(-70J/C/9m)= 7,8N/C.
En la gráfica (E, r), dado que V = -I E dr , la diferencia de potencial entre dos puntos sería el área
abarcada entre ellos, en este caso, entre 2 y 4m, es de 40V (fig.56) que coincide
con la diferencia de potencial entre 2 y 4 metros en la gráfica (V, r) de
la fig.55.
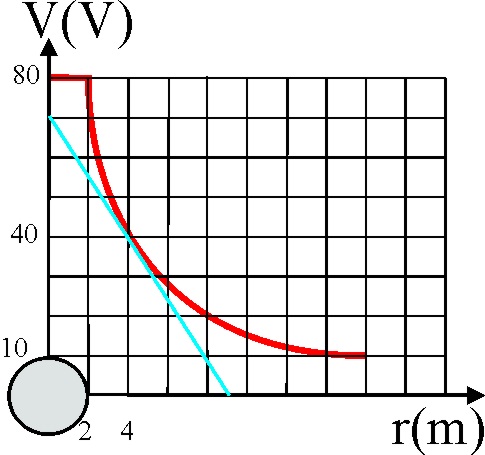
Fig.55
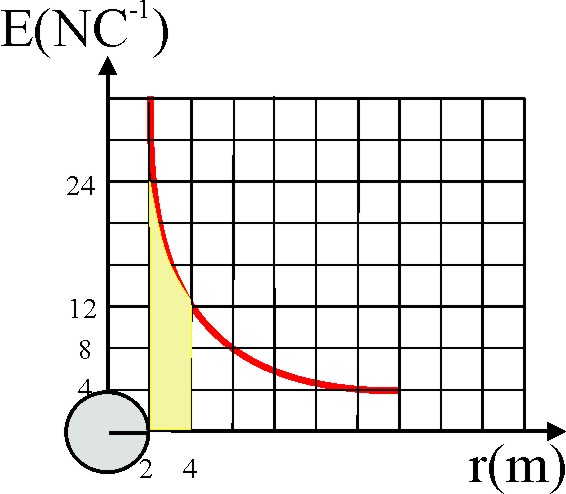
Fig.56
Para Maxwell, lo que llamaba “curl”
(bucle, rizo o rotor) de un campo de fuerzas, expresaba “el par de rotación que se ejercía sobre las bolas eléctricas situadas
en un punto del campo”, suponiendo que había 1/2p bolas eléctricas por unidad de superficie de los remolinos magnéticos.
Sin embargo no lo llama rotacional. En el mismo trabajo en el que define
la convergencia del cuaternión
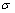 =it+ju+kv, al efectuar la operación
=it+ju+kv, al efectuar la operación
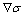 =S
=S
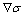 + V
+ V
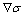 , como el primer término cambiado de signo. El segundo término que implica
la operación:
, como el primer término cambiado de signo. El segundo término que implica
la operación:
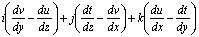 , lo llama “curl” o “version”
, que se podría traducir por rotor o vuelta. En carta al profesor Tait,
le dice : “La parte escalar la llamaría convergencia del vector función, y la parte vectorial la llamaría el
“curl” (bucle) del vector función. Aquí el término bucle no tiene nada que ver con un tornillo o hélice. La palabra “turn” o “version” (vuelta) a su vez sería mejor que la palabra “twist” (giro), porque
giro sugiere un tornillo. La palabra “curl” (bucle o rotor) está libre de
la noción de rosca y es suficientemente clásica, aunque demasiado moderna para los matemáticos puros,
así que por el bien de Cayley (matemático de la época de Maxwell) podría decir “curl” (rotor) (en la costumbre
de enrollarse)”
, lo llama “curl” o “version”
, que se podría traducir por rotor o vuelta. En carta al profesor Tait,
le dice : “La parte escalar la llamaría convergencia del vector función, y la parte vectorial la llamaría el
“curl” (bucle) del vector función. Aquí el término bucle no tiene nada que ver con un tornillo o hélice. La palabra “turn” o “version” (vuelta) a su vez sería mejor que la palabra “twist” (giro), porque
giro sugiere un tornillo. La palabra “curl” (bucle o rotor) está libre de
la noción de rosca y es suficientemente clásica, aunque demasiado moderna para los matemáticos puros,
así que por el bien de Cayley (matemático de la época de Maxwell) podría decir “curl” (rotor) (en la costumbre
de enrollarse)”
![]() ), se define la CIRCULACIÓN DE DICHO VECTOR como:
), se define la CIRCULACIÓN DE DICHO VECTOR como: ![]() (19)
(19)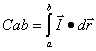 (20)
(20)![]() (muchas veces se reserva
el nombre de CIRCULACIÓN específicamente para este recorrido, aplicando el
de PROCESIÓN, cuando es abierto).
(muchas veces se reserva
el nombre de CIRCULACIÓN específicamente para este recorrido, aplicando el
de PROCESIÓN, cuando es abierto).![]() , al sustituir en la expresión
, al sustituir en la expresión
![]() . Al definirse el trabajo
W como
. Al definirse el trabajo
W como
![]() , tendremos que la circulación del vector campo
no es más que:
, tendremos que la circulación del vector campo
no es más que: ![]() desde A hasta B, y luego desde B hasta A en el dibujo dado (fig.42)
desde A hasta B, y luego desde B hasta A en el dibujo dado (fig.42)








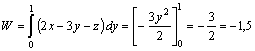
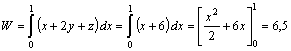 .
.